Electric Potential Due to a Point Charge

We already have an introduction of work and energy while studying mechanics.
We know that central forces are conservative in nature i.e., work done on any particle moving under the influence of consrevative forces does not depend on path taken by the particle but depends on initial and final positions of the particle.
Electrostatic force given by Coulumb’s law is also a central force like gravitational force and is conservative in nature.
For conservative forces, work done on particle undergoing displacement can be expressed in terms of potential energy function.
In this chapter we will apply work and energy considerations to the electric field and would develop the concept of electric potential energy and electric potential.

Electric potential energy

Consider a system of two point charges in which positive test charge q’ moves in the field produced by stationary point charge q shown below in the figure.
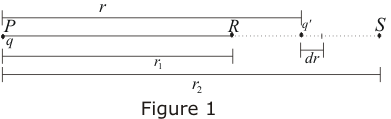
Charge q is fixed at point P and is displaced from point R to S along a radial line PRS shown in the figure.
Let r₁ be the distance between points P and R and r₂ be the distance between P and S.
The magnitude of force on positive test charge as given by Coulomb’s law is
If q’ moves towards S through a small displacement dr then work done by this force in making the small displacement dr is
dW=F·dr
Total work done by this force as test charge moves from point R to S i.e., from r₁ to r₂ is,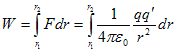or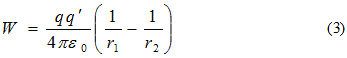
Thus for this particular path work done on test charge q’ depends on end points not on the path taken.
Work done W in moving the test charge q’ from point R to S is equal to the change in potential energy in moving the test charge q’ from point R to S. Thus,
W=U(r₁)-U(r₂) (4)
where
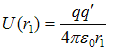is the potential energy of test charge q’ when it is at point R and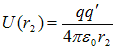is the potential energy of test charge q’ when it is at point S.
Thus potential energy of test charge q’ at any distance r from charge q is given by
Equation 5 gives the electric potential energy of a pair of charges which depends on the separation between the charges not on the location of charged particles.
If we bring the test charge q’ from a very large distance such that r₂=∞ to some distance r₁=r then we must do work against electric forces which is equal to increase in potential energy as given by equation 5.
Thus potential energy of a test charge at any point in the electric field is the work done against the electric forces to bring the charge from infinity to point under consideration.

Electric Potential

We now move towards the electric potential which is potential energy per unit charge.
Thus electrostatic potential at any point of an electric field is defined as potential energy per unit charge at that point.
Electric potential is represented by letter V.
V=U/q’ or U=q’V (6)
Electric potential is a scalar quantity since both charge and potential energy are scalar quantities.
S.I. unit of electric potential is Volt which is equal to Joule per Coulumb. Thus,
1 Volt = 1 JC^-1
In equation 4 if we divide both sides by q’ we have
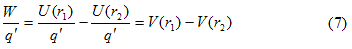where V(r₁) is the potential energy per unit charge at point R and V<r_{2) is potential energy per unit charge at point S and are known as potential at points R and S respectively.

</r}
Again consider figure 1. If point S in figure 1 would be at infinity then from equation 7
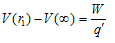Since potential energy at infinity is zero therefore V(∞)=0. Therefore
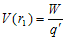hence electric potential at a point in an electric field is the ratio of work done in bringing test charge from infinity to that point to the magnitude of test charge.
Dimensions of electric potential are [ML²T^-3A^-1] and can be calculated easily using the concepts of dimension analysis.

Electric potential due to a point charge

Consider a positive test charge +q is placed at point O shown below in the figure.
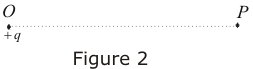
We have to find the electric potential at point P at a distance r from point O.
If we move a positive test charge q’ from infinity to point P then change in electric potential energy would be

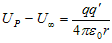
The electric potential at point P is

Potential V at any point due to an arbitrary collection of point charges is given by

here we see that like electric field potential at any point independent of test charge used to define it.
For continuous charge distributions summation in above expression will be replaced by the integration

where dq is the differential element of charge distribution and r is its distance from the point at which V is to be calculated.

Relation between electric fields and electric potential

Consider the electric field E due to a point charge +q at point O in a radially outward direction shown below in the figure.

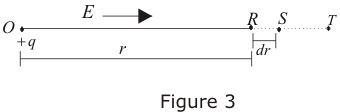
Suppose R and S are two points at a distance r and r+dr from point O where dr is vanishingly small distance and V is electric potential at point R.
Now force on any test charge q’ at point R in terms of electric field is
F=q’E
Work done by the force in displacing test charge from R to S in field of charge q is
dW = F·dr = q’E·dr
and, change in potential energy is
dU = -dW = -q’E·dr
Change in electric potential would be
dV = dU/q
or dV = –E·dr (11)
From equation 11 electric field is
E=-(dV/dr) (12)
the quantity dV/dr is the rate of change of potential with the distance and is known as potential gradient. Negative sign in equation 12 indicates the decrease in electric potential in the direction of electric field.
For cartesian coordinate system
E=E_xi+E_yj+E_zk
and,
dr=dxi+dyj+dzk
from equation 11
dV=-E⋅dr
or, dV=-(E_xdx+E_ydy+E_zdz) (13)
Thus components of E are related to corresponding derivatives of V in the following manner
E_x=dV/dx                                          (14a)
E_y=dV/dy                                          (14b)
E_z=dV/dz                                          (14c)
In equation (14a) we see that V is differentiated with respect to coordinate x keeping other coordinates constant. Same is the case with equations (14b) and (14c) in case of y and z coordinates respectively.

Equipotential surfaces

Surface over which the electric potential is same everywhere is called an equipotential surface.
Equipotential surfaces are graphical way to represent potential distribution in an electric field.
We can draw equipotential surfaces through a space having electric field.
For a positive charge , electric field would be in radially outward direction and the equipotential surfaces would be concentric spheres with centers at the charge as shown below in the figure.

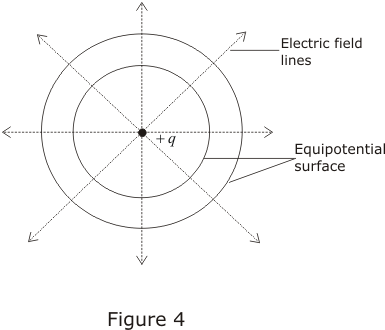
Since electric potential remains same everywhere on an equipotential surface from this it follows that PE of a charged body is same at all points on this surface. This shows that work done in moving a charged body between two points on an equipotential surface would be zero.
At every point on equipotential surface, electric field lines are perpendicular to the surface. This is because potential gradient along any direction parallel to the surface is zero i.e.,
E=-dV/dr=0
so component electric parallel to equipotential surface is zero.

Potential due to an electric dipole

We already know that electric dipole is an arrangement which consists of two equal and opposite charges +q and -q separated by a small distance 2a.
Electric dipole moment is represented by a vector p of magnitude 2qa and this vector points in direction from -q to +q.
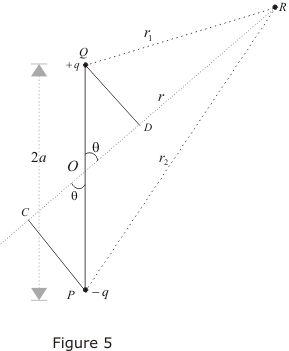
To find electric potential due to a dipole consider charge -q is placed at point P and charge +q is placed at point Q as shown below in the figure.
Since electric potential obeys superposition principle so potential due to electric dipole as a whole would be sum of potential due to both the charges +q and -q. Thus

where r₁ and r₂ respectively are distance of charge +q and -q from point R.

Now draw line PC perpandicular to RO and line QD perpandicular to RO as shown in figure. From triangle POC
cosθ=OC/OP = OC/a
therefore OC=acosθ similarly OD=acosθ
Now ,
r₁ = QR≅RD = OR-OD = r-acosθ
r₂ = PR≅RC = OR+OC = r+acosθ

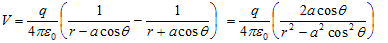
since magnitude of dipole is
|p| = 2qa

If we consider the case where r>>a then

again since pcosθ= p·rˆ where, rˆ is the unit vector along the vector OR then electric potential of dipole is

for r>>a

From above equation, we can see that potential due to the electric dipole is inversly proportional to r² not ad 1/r which is the case for potential due to single charge.
Potential due to electric dipole does not only depends on r but also depends on angle between position vector r and dipole moment p.

Work done in rotating an electric dipole in an electric field

Consider a dipole placed in a uniform electric field and it is in equilibrium position. If we rotate this dipole from its equilibrium position, work has to be done.
Suppose electric dipole of moment p is rotated in uniform electric field E through an angle θ from its equilibrium position. Due to this rotation couple acting on dipole changes.
If at any instant dipole makes an angle φ with uniform electric field then torque acting on dipole is
Γ=pEsinφ (19)
again work done in rotating this dipole through an infitesimaly small angle dφ is
dW=torque x angular displacement
=pEsinφdφ
Total work done in rotating the dipole through an angle θfrom its equilibrium position is

This is the required formula for work done in rotating an electric dipole placed in uniform electric field through an angle θ from its equilibrium position.

The potential energy of dipole placed in the uniform electric field

Again consider equation 20 which gives the work done in rotating electric dipole through an infinitesimally small angle dφ is
dW=pEsinφdφ
which is equal to the change in potential energy of the system
dW=dU=pEsinφdφ (22)
If angle dφ is changed from 90⁰ to θ then in potential energy would be

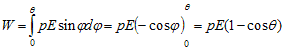
We have chosen the value of φgoing from π/2 to θ because at π/2 we can take potential energy to be zero (axis of the dipole is perpendicular to the field). Thus U(90⁰)=0 and above equation becomes

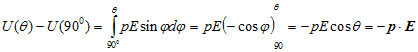
Type of Questions can be asked in the Board Examination

Define electric potential and electric potential difference. How do they relate to a point charge?
Explain the concept of electric potential due to a point charge. How does the distance from the charge affect the electric potential?
Calculate the electric potential at a point P located at a distance of r meters from a point charge of q coulombs. Use the formula ,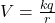 $V = \frac{kq}{r}$
where k is Coulomb’s constant.
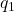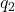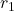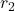Given two point charges, ${q_1}$ and ${q_2}$ , at distances ${r_1}$ and ${r_2}$ respectively from a common point, calculate the net electric potential at that point.
Compare the electric potential due to a point charge at two different points located at distances r1 and r2 from the charge. Which point has a higher potential and why?
A point charge q is placed at the origin. Calculate the work done in moving a smaller charge q0 from point A to point B along a field line. How does this work relate to the change in electric potential?
Describe how the concept of electric potential due to a point charge is applied in determining the potential energy of a system of charges.
Sketch a graph showing the variation of electric potential due to a point charge as a function of distance from the charge. Explain the features of the graph.
Why is the electric potential considered a scalar quantity, and how does this property simplify the calculation of potential due to multiple charges?
A test charge q0 experiences an electric force due to a point charge q. If the test charge is moved closer to the point charge, how does the electric potential energy of the system change? Calculate the change in potential energy if specific distances are given.